Rhino's Blog
0%

Posted on

主机设置

主机的小飞机需要勾选，选项设置->本地代理->允许来自局域网的连接。

设置图片

虚拟机设置

看到一些博客说，虚拟机一定要设置为桥接模式，实际上是任何模式都行，只要虚拟机能够ping通主机的ip地址。就能使用主机的代理。

在bashrc下设置终端程序走代理, 填主机的ip和小飞机监听的端口。

1
2
export http_proxy=http://address:port
export https_proxy=https://address:port

设置应用程序走代理：
ubuntu设置全局代理

Posted on Edited on

一般的模型的加载在LeanOpenGL里已经讲解得比较清楚了，本博文是介绍如何在LeanOpenGL示例Mesh.h，和Model.h基础之上扩展，使其支持骨骼动画的播放。

骨骼动画的原理

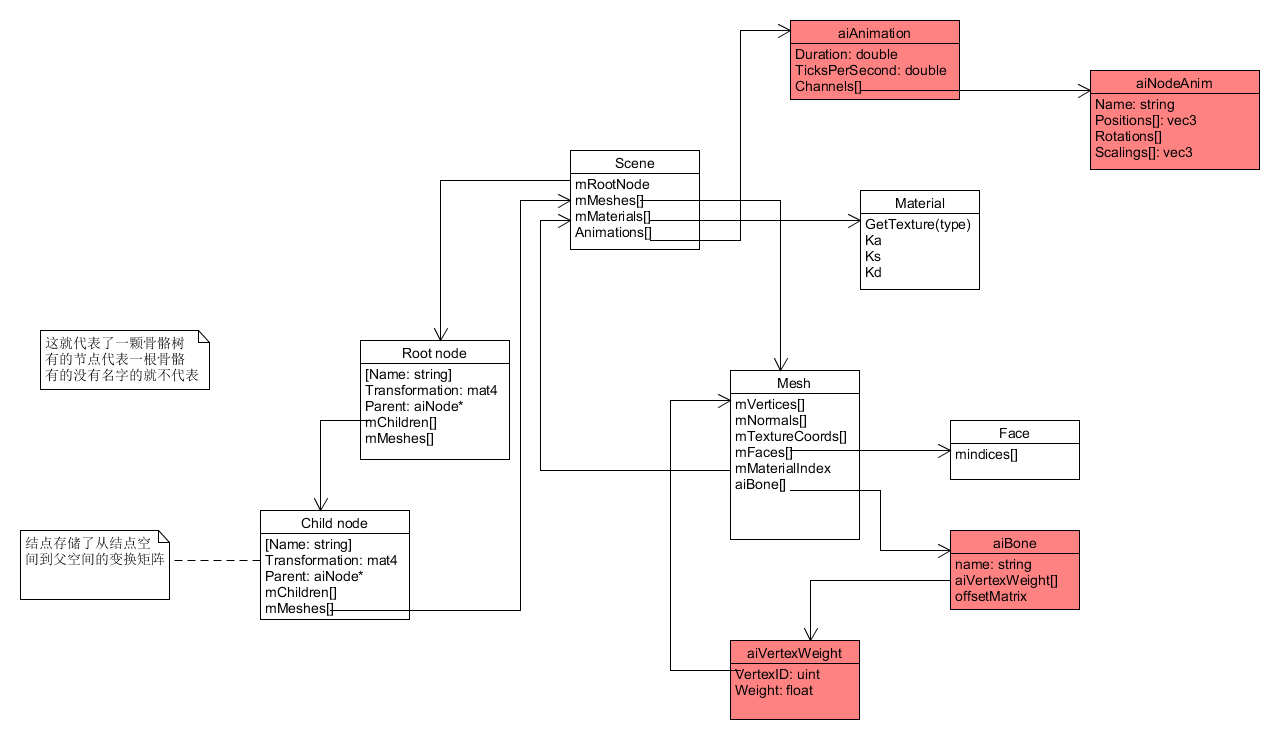
Assimp数据结构

带有骨骼动画的模型除了有skin（即一系列的网格），还有骨骼aiBone和动画aiAnimation。骨骼没有大小和位置，只有一个名字和初始旋转矩阵（决定了骨骼的初始姿态），除此之外，每一个骨骼还存储了它所影响的顶点的ID以及影响的权重；动画aiAnimation存储了一系列的关键帧和当前动画的持续时间。关键帧存储的是从初始姿态到当前姿态，所有骨骼要经过的旋转平移和缩放。

在骨骼动画播放的时候，首先根据当前时间找到动画的前一个关键帧和后一个关键帧，然后根据到这两个关键帧的时间距离进行线性插值，得到当前关键帧。再将当前关键帧的旋转平移和缩放应用到所有相关的骨骼上，从而改变当前的骨骼姿态。

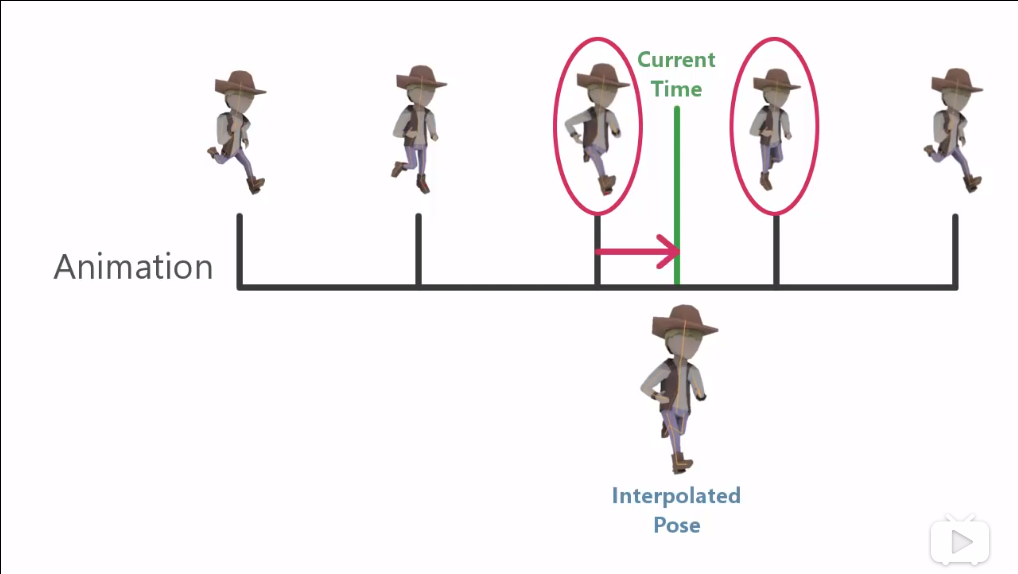
骨骼动画播放

最后在着色器中，将骨骼当前的姿态，按照权重作用到受其影响的顶点上，从而改变顶点的位置。

骨骼相关数据的加载

扩展Mesh中的顶点结构体：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#define BONE_INFO_NUM 4

struct Vertex {
	// position
	glm::vec3 Position;
	// normal
	glm::vec3 Normal;
    // 这里的注释是因为项目中使用的都是多边形的模型，并没有纹理贴图，所以去掉了
	//// texCoords
	//glm::vec2 TexCoords;
	//// tangent
	//glm::vec3 Tangent;
	//// bitangent
	//glm::vec3 Bitangent;
	glm::ivec4 boneID; //影响骨骼ID

	glm::vec4 boneWeight; // 对应权重

	Vertex() {
		Position = glm::vec3(0.0f, 0.0f, 0.0f);
		Normal = glm::vec3(0.0f, 0.0f, 0.0f);
		boneID = glm::ivec4(-1, 0, 0, 0);
		boneWeight = glm::vec4(0.0f, 0.0f, 0.0f, 0.0f);
	}

	void AddBoneData(uint BoneID, float Weight) {
		for (unsigned int i = 0; i < BONE_INFO_NUM; i++) {
			if (Weight > boneWeight[i]) {
				for (unsigned int j = BONE_INFO_NUM - 1; j > i; j--) {
					boneWeight[j] = boneWeight[j - 1];
					boneID[j] = boneID[j - 1];
				}
				boneWeight[i] = Weight;
				boneID[i] = BoneID;
				break;
			}
		}
	}

	void normalizeBoneWeight() {
		float totalWeight = boneWeight.x + boneWeight.y + boneWeight.z + boneWeight.w;
		boneWeight.x = boneWeight.x / totalWeight;
		boneWeight.y = boneWeight.y / totalWeight;
		boneWeight.z = boneWeight.z / totalWeight;
		boneWeight.w = boneWeight.w / totalWeight;
	}


};

顶点记录了影响它的骨骼的IDboneID，和对应的权重boneWeight，影响顶点的骨骼数量是没有上限的，在这里我们只取影响最大的4个骨骼。这里要注意的是，只取最大的四个，最后他们的权重和并不为1，导致在播放骨骼动画的时候，模型会变形，所以在所有骨骼都处理完毕之后，要对每一个顶点执行normalizeBoneWeight函数，使它们的权重值和为1。

加载骨骼数据并归一化

在加载完Mesh的其他数据的时候，遍历Mesh中的所有骨骼，将骨骼的ID和权重添加到对应的顶点的属性中，这里参照ogldev教程（参考3）的做法，所有Mesh的骨骼是存在一起的，这样方便最后一次性将所有骨骼的姿态传入着色器。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 加载骨骼权重信息到顶点，并将骨骼加入allBones和boneMap
for (uint i = 0; i < mesh->mNumBones; i++) {
	unsigned int BoneIndex = 0;
	string BoneName(mesh->mBones[i]->mName.data);
	if (boneMap.find(BoneName) == boneMap.end()) {
		// Allocate an index for a new bone
		BoneIndex = numBones;
		numBones++;
		Bone tmpBone;
		tmpBone.boneOffset = mesh->mBones[i]->mOffsetMatrix;
		tmpBone.name = BoneName;
		// 加入map
		boneMap[BoneName] = BoneIndex;
		// 加入allBones
		allBones.push_back(tmpBone);
	}
	else {
		BoneIndex = boneMap[BoneName];
	}
	for (uint j = 0; j < mesh->mBones[i]->mNumWeights; j++) {
		unsigned int vertexID = mesh->mBones[i]->mWeights[j].mVertexId;
		float weight = mesh->mBones[i]->mWeights[j].mWeight;
		// 给vertices添加影响骨骼信息
		vertices[vertexID].AddBoneData(BoneIndex, weight);
	}
}
// 所有的骨骼都加上影响权重之后
for (auto& vertex : vertices) {
	vertex.normalizeBoneWeight();
}

骨骼动画的渲染

计算当前帧

以下直接直接复用了ogldev教程的源码

这里设置的动画是循环播放的，所以将当前时间以模型持续时间取模，计算出动画的时间位置。

骨骼是一个树的结构，骨骼树的信息存储在以Scene->mRootNode为根节点的树中，如果当前node的mName不为空，那么它就代表一根骨骼，node的childNode就是它的子骨骼。因为父骨骼的姿态要影响到子骨骼的姿态（如大腿骨移动，小腿骨骼也要跟着移动），所以要从根节点开始，一层一层递归地计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void BoneTransform(float TimeInSeconds, vector<Matrix4f>& Transforms)
{
	Matrix4f Identity;
	Identity.InitIdentity();

	float TicksPerSecond = (float)(pScene->mAnimations[0]->mTicksPerSecond != 0 ? pScene->mAnimations[0]->mTicksPerSecond : 25.0f);
	float TimeInTicks = TimeInSeconds * TicksPerSecond;
	float AnimationTime = fmod(TimeInTicks, (float)pScene->mAnimations[0]->mDuration);

	ReadNodeHeirarchy(AnimationTime, pScene->mRootNode, Identity);

	Transforms.resize(numBones);

	for (uint i = 0; i < numBones; i++) {
		Transforms[i] = allBones[i].FinalTransformation;
	}
}

根据当前时间找出当前的前一帧和后一帧，再根据时间差线性插值，计算出的平移，旋转和缩放并结合父骨骼的变换作用到当前骨骼上，最后将计算好的当前骨骼的姿态作为父骨骼的变换，递归地处理所有子骨骼：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
void ReadNodeHeirarchy(float AnimationTime, const aiNode* pNode, const Matrix4f& ParentTransform)
{
	string NodeName(pNode->mName.data);

	const aiAnimation* pAnimation = pScene->mAnimations[0]; //选择动画

	Matrix4f NodeTransformation(pNode->mTransformation);

	const aiNodeAnim* pNodeAnim = FindNodeAnim(pAnimation, NodeName);

	if (pNodeAnim) {
		// Interpolate scaling and generate scaling transformation matrix
		aiVector3D Scaling;
		CalcInterpolatedScaling(Scaling, AnimationTime, pNodeAnim);
		// 因为我们项目中的动画没有涉及到大小形变，且有的模型动画自带x100的放大，播放动画的时候会变得非常的大，所以这里将骨骼动画的形变量忽略
            // 忽略scale影响
		Matrix4f ScalingM;
		//ScalingM.InitIdentity();
		ScalingM.InitScaleTransform(Scaling.x, Scaling.y, Scaling.z);

		// Interpolate rotation and generate rotation transformation matrix
		aiQuaternion RotationQ;
		CalcInterpolatedRotation(RotationQ, AnimationTime, pNodeAnim);
		Matrix4f RotationM = Matrix4f(RotationQ.GetMatrix());

		// Interpolate translation and generate translation transformation matrix
		aiVector3D Translation;
		CalcInterpolatedPosition(Translation, AnimationTime, pNodeAnim);
		Matrix4f TranslationM;
		TranslationM.InitTranslationTransform(Translation.x, Translation.y, Translation.z);

		// Combine the above transformations
		NodeTransformation = TranslationM * RotationM * ScalingM;
	}

	Matrix4f GlobalTransformation = ParentTransform * NodeTransformation;

	if (boneMap.find(NodeName) != boneMap.end()) {
		uint BoneIndex = boneMap[NodeName];
		allBones[BoneIndex].FinalTransformation = globalInverseTransform * GlobalTransformation * allBones[BoneIndex].boneOffset;
	}
	// 递归处理所有子骨骼
	for (uint i = 0; i < pNode->mNumChildren; i++) {
		ReadNodeHeirarchy(AnimationTime, pNode->mChildren[i], GlobalTransformation);
	}
}

将骨骼姿态作用在顶点上

最后将计算好的所有的骨骼姿态传入着色器中：

1
2
3
4
5
6
BoneTransform(time, Transforms);
for (unsigned int i = 0; i < numBones; i++) {
    sprintf(uniformName, "gBones[%d]", i);
    GLuint location = glGetUniformLocation(shader.ID, uniformName);
    glUniformMatrix4fv(location, 1, GL_TRUE, (const GLfloat*)Transforms[i]);
}

在着色器中，先根据顶点受影响的骨骼ID和权重，计算出当前顶点受骨骼姿态的影响矩阵BoneTransform，顶点在乘以Model，View，Projection矩阵前，先乘以BoneTransform矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in ivec4 BoneIDs;
layout (location = 3) in vec4 Weights;

...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

... 
const int MAX_BONES = 100;
uniform mat4 gBones[MAX_BONES];

void main()
{
	mat4 BoneTransform = mat4(1.0);
    BoneTransform = gBones[BoneIDs[0]] * Weights[0];
    BoneTransform     += gBones[BoneIDs[1]] * Weights[1];
    BoneTransform     += gBones[BoneIDs[2]] * Weights[2];
    BoneTransform     += gBones[BoneIDs[3]] * Weights[3];
    vs_out.FragPos = vec3(model * BoneTransform * vec4(aPos, 1.0));
	...
    gl_Position = projection * view * vec4(vs_out.FragPos, 1.0);
}

Code

扩展后完整的Mesh和Model

参考

Posted on Edited on

​ 系统分析与设计课程项目终于完结撒花了。我在项目中主要负责小程序的后端部分，在项目规划阶段，我们后端组无意间看到了小程序云开发

  • 数据库：一个既可在小程序前端操作，也能在云函数中读写的 JSON 文档型数据库
  • 文件存储：在小程序前端直接上传/下载云端文件，在云开发控制台可视化管理
  • 云函数：在云端运行的代码，微信私有协议天然鉴权，开发者只需编写业务逻辑代码

看到如此好处，秉持着尝试新鲜技术的精神（懒），我们项目的后端决定采用小程序云开发来实现，从开始感叹它的方便，到中期遇到了种种问题差点放弃改用传统服务器后端，到最后成功做完，这里总结一下经过这几个月的开发，我所理解的小程序云开发的优点和缺点。

优点

  • 小程序云开发不需要另外租一个服务器

这个好处还是蛮明显的，小程序开发本身是不需要花费任何钱的，使用云开发服务端的费用也省去，整个开发过程就只有时间成本，完全可以使用云开发小程序做一个人的练手项目。

  • 用户无需登入

传统服务器后端确定用户身份是有些复杂的，这就需要根据官方微信小程序的登入流程去走，一系列巴拉巴拉。

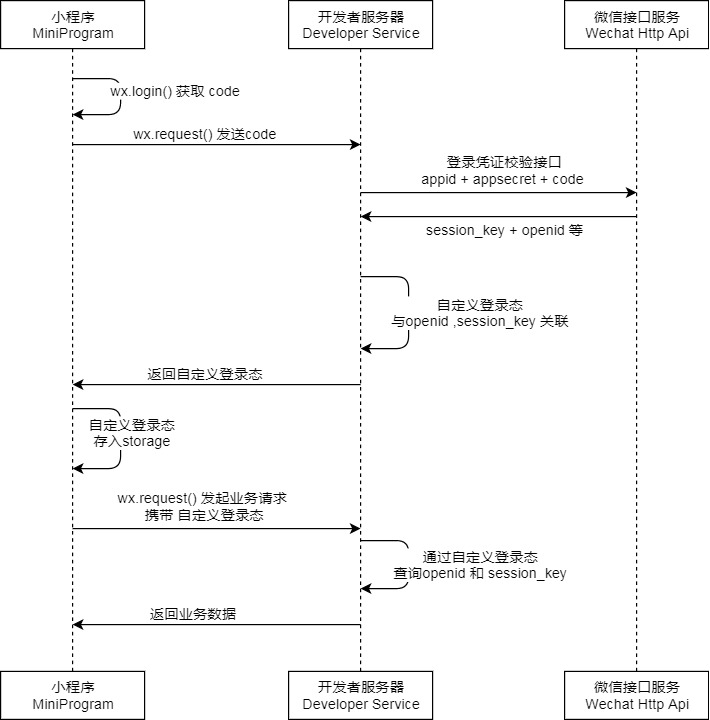
而云函数的参数就能直接确定用户的身份：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// index.js 是入口文件，云函数被调用时会执行该文件导出的 main 方法
// event 包含了调用端（小程序端）调用该函数时传过来的参数，同时还包含了可以通过 getWXContext 方法获取的用户登录态 `openId` 和小程序 `appId` 信息
const cloud = require('wx-server-sdk')
exports.main = (event, context) => {
  let { userInfo, a, b} = event
  let { OPENID, APPID } = cloud.getWXContext() // 这里获取到的 openId 和 appId 是可信的
  let sum = a + b

  return {
    OPENID,
    APPID,
    sum
  }
}

这种种的方便确实使得后端开发的工作量大大减少（因为过于方便，所以后面没事做了也参与了小程序页面的开发Orz)

  • 方便的日志功能

每一次云函数的调用都能在云开发控制台查看调用日志，在云函数中使用console.log就能输出自定义的日志，在决定后端代码开发规范的时候，我们就决定云函数要在输出关键信息，这样的日志输出方面我们在前端返回没有按照预期的时候，能够还原当时云函数的环境，迅速排查错误。

缺点

  • 小程序云开发的服务器不在自己的掌控之中

云开发后端的性能难以保证，在网上也没有找到具体的说明。且云函数、云数据库、云文件存储的每月调用次数是有限制的。且在开发的几个月中，也遇到过偶尔无法调用云函数的情况，这要看腾讯的实力了。要想确保性能还是要有一个自己的服务器比较安心。前期使用云开发试水，获得不错反响后再换成传统服务器也是不错的方案。

  • 前端直接使用函数调用的方式，难以遵循RESTful规范

因为是前端直接函数调用，不需要使用URL，只能通过云函数的名字来表示函数的功能，这是面向操作，而不是RESTful所倡导的面向资源。

比如我们获得所有问卷的云函数get_questionnaire，是以动词开头表明是获取，后面才是我们要获取的资源。这样的命名方法导致我们还有fill_in_questionnaire，get_questionnaire_detail的云函数，目前我们只有21个云函数，就已经感觉有一些紊乱了，难以应对大型项目。（PS：项目最后我们想到可以每一个资源有一个Router云函数，再通过参数的调用其他云函数处理，但无奈已经写完了，DDL也到了，没有时间重构）

而根据RESTful设计出来的API就可以是用GET、POST、DELETE方法访问xxx/questionnaire就能够完成各种针对问卷资源的操作，通过服务端的Router将请求导航到不同的处理函数，使得前端的调用比较简单易理解，后端的处理也更有条理，更易于维护。

总结

云开发还是比较香的，当前的小程序完全可以先使用云开发，加快开发周期，如果项目成功，再换回传统的服务器来支持更多的用户以及更好的响应速度和稳定性。

Posted on Edited on

1.存在的意义

在使用一般指针编程的时候会出现的几种错误：

  1. 使用new申请堆空间忘记delete
  2. delete之前发生异常，不正常结束，跳过delete
  3. 当多线程使用指向同一个堆地址的指针，不知道本线程退出时是否应该delete，以及是使用时否已经delete

2.通用的实现方法

使用一个类，类的成员变量中有一根指针ptr，类重载指针的操作：解引用*()，调用->，在析构的时候delete ptr。

存在的问题：多个智能指针指向同一个堆地址，第一个智能指针析构后，后面的指针析构时就会发生重复delete。

解决方案：

  1. 定义赋值运算符，使之执行深复制。这样两个指针将指向不同的对象，其中的一个对象是另一个对象的副本。（赋值后指向的地址不再相同，失去指针意义）
  2. 建立所有权（ownership）概念，对于特定的对象，只能有一个智能指针可拥有它，这样只有拥有对象的智能指针的构造函数会删除该对象。然后，让赋值操作转让所有权。这就是用于auto_ptr和unique_ptr的策略，但unique_ptr的策略更严格。
  3. 创建智能更高的指针，跟踪引用特定对象的智能指针数。这称为引用计数（reference counting）。例如，赋值时，计数将加1，而指针过期时，计数将减1。仅当最后一个指针过期时，才调用delete。这是shared_ptr采用的策略。

3.auto_ptr & unique_ptr

unique_ptr 可以传入new[] 返回的指针，在定义的时候需要加上[]（只有unique_ptr可以使用new[] ）(问题：shared_ptr vs2017中也可以使用new [])。如： 

1
2
unique_ptr<double[]> pad(new double[5]);
pad[3] = 3.9; //像数组一样访问

pic1

auto_ptr是c++98标准中的（c++11弃用），unique_ptr是c++11标准中的。

auto_ptr 能够赋值给auto_ptr, 而unique_ptr不能赋值给unique_ptr（但是右值unique_ptr能够赋值给unique_ptr）。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <memory>
#include <string>
using namespace std;

unique_ptr<string> demo1(string s) {
	return unique_ptr<string> (new string(s));
}

auto_ptr<string> demo2(string s) {
	return auto_ptr<string>(new string(s));
}

int main() {
	string *s1 = new string("some words");
	unique_ptr<string> up1(s1);
	//unique_ptr<string> up2 = up1;  编译不通过
	unique_ptr<string> up2 = unique_ptr<string>(new string("some words"));
   // 允许，临时变量为右值
   unique_ptr<string> up3 = demo1("some words");
   // 允许，值返回的临时变量为右值
   
	string *s2 = new string("some words");
	auto_ptr<string> ap1(s2);
	auto_ptr<string> ap2 = ap1;
   // 允许，但ap1已经失去s2的所有权
	auto_ptr<string> ap3 = auto_ptr<string>(new string("some words"));
	auto_ptr<string> ap4 = demo2("some words");

	cout << *ap1 << endl; // 运行时出错
	system("pause");
}

4. shared_ptr

shared_ptr中有两个指针：

  1. 构造时传入的指针
  2. 指向控制块的指针

在shared_ptr拷贝构造或者赋值的时候（如shared_ptr<int>a = b），a的控制块指针指向b的控制块，并将控制块中的引用次数+1（原子操作）。

由实现可以看出，共享多个shared_ptr，一定要是： 

1
2
3
4
5
6
7
8
int *num = new int(6);
shared_ptr<int> old_ptr(num);
//成功共享
shared_ptr<int> new_ptr = old_ptr;
shared_ptr<int> new_ptr(old_ptr);

//错误共享
shared_ptr<int> new_ptr<num>

line8中的构造方式，new_ptr和old_ptr的控制块并不是同一个，因此会发生多次析构的问题。

shared_ptr的循环引用问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
#include <memory>
#include <string>
using namespace std;

unique_ptr<string> demo1(string s) {
	return unique_ptr<string> (new string(s));
}

auto_ptr<string> demo2(string s) {
	return auto_ptr<string>(new string(s));
}

struct structA;
struct structB;

struct structA
{
	shared_ptr<structB> Aptr;
	~structA() { cout << "deconstruct  A" << endl; }
};

struct structB
{
	shared_ptr<structA> Bptr;
	~structB() { cout << "deconstruct  B" << endl; }
};

int main() {
	{
		shared_ptr<structA> ap(new structA);
		{
			shared_ptr<structB> bp(new structB);
			cout << ap.use_count() << endl;
			cout << bp.use_count() << endl;
			cout << ap->Aptr.use_count() << endl;
			cout << bp->Bptr.use_count() << endl;

			ap->Aptr = bp;
			bp->Bptr = ap;
			cout << endl;


			cout << ap.use_count() << endl;
			cout << bp.use_count() << endl;
			cout << ap->Aptr.use_count() << endl;
			cout << bp->Bptr.use_count() << endl;
		}
		cout << endl;
		cout << ap.use_count() << endl;
		cout << ap->Aptr.use_count() << endl;
	}

	system("pause");
}
/*
输出：
1
1
0
0

2
2
2
2

2
1
*/
  1. 可以看到，在39~40的操作之后，4个智能指针的引用计数器都为2。
  2. 在48行bp析构的时候，因为Aptr还在指向structB，只有bp被析构，bp指向的structB并没有从堆中析构。
  3. 因为structB没有从堆中析构，Bptr仍然指向structA，所以ap析构的时候，ap指向的structA也不会从堆中析构。
  4. 最后情况是堆中既有structA，也有structB，他们的指针的引用计数都为1，内存泄露发生。

循环引用的避免：

  1. 将其中一个shared_ptr改为weak_ptr（weak_ptr只是一种编译时的循环引用解决方案，如果运行时发生，依然会造成内存泄露）。
  2. 设计时避免循环引用

5. weak_ptr

使用较少，暂不探索

参考

Posted on Edited on

new和delete是一个表达式，执行的过程中会被分解。

new和delete的分解

单个对象的new和delete

表达式String* ps = new String("hello");会被分解为

1
2
3
void* mem = operator new(sizeof(String)) //在这个内部调用了malloc
ps = static_cast<String*>(mem); //类型的转换
ps->String::String("hello");  //显示地调用构造函数

表达式delete ps;会被分解为

1
2
ps->String::~String(); //显示调用析构函数
operator delete(ps); // 释放内存，内部调用free

对象数组的new和delete

表达式String* ps = new String[5]; 会被分解为

1
2
3
4
5
6
void* mem = operator new(sizeof(String) * 5 + 4); 
//new一个数组的时候会有一个int来存储数组的大小
ps = static_cast<String*>(mem);
ps->String();
(ps + 1)->String();
....//共调用五次

表达式delete[] ps; 会被分解为

1
2
3
4
ps->String::~String(); //显示调用析构函数
(ps + 1)->String::~String();
...//共调用五次
operator delete(ps); // 释放内存，内部调用free

由此，如果申请了一个对象数组(new[])，却使用 delete删除，那么只会调用第一个对象的析构函数，未调用析构函数的对象之前如果申请了堆空间，就会发生内存泄露。

new和delete的重载

在对象的public成员函数中重载(可以是static)，可以自定义对象的new的过程，用于内存池：大致就是重载的operator new中不使用malloc而是返回一个已分配好了的内存的指针，operator delete中不使用free，而是将内存返回给内存池，整个过程不向系统索要内存返还内存，没有用户态到系统态的切换，更加快速。

1
2
3
4
5
6
7
8
class Foo {
    public:
    void* operator new(size_t);
    void operator delete(void*, size_t); //size_t可有可无
    
    void* operator new[](size_t);
    void operator delete[](void*, size_t); //size_t可有可无    
}

此后new Foo, delete Foo, new Foo[n], delete[] p就会使用自定义的操作了。

如果重载了new和delete却不想使用，可以::new和::delete调用默认的operator new和operator delete。

参考 侯捷 C++程序设计

Posted on Edited on

逻辑时钟系统的概念

在分布式系统中，因为网络的延迟，两台计算机无法拥有一致的时钟（每台计算机之间的时钟看上去只有微小的偏差，但在现代计算机CPU以GHZ为单位计算的频率面前，就是无法容忍的误差了），由于无法拥有一致的时钟，人们使用逻辑时钟来表达，记录分布式系统中的时间。

一个逻辑时钟系统由一个时间域$T$和映射关系$C$组成。

  • T是一个集合，它包含了所有事件发生的逻辑时间，在分布式系统中并不是所有的事件的发生都确定先后关系，所以集合内的元素一般呈现偏序关系。
  • 映射关系$C​$将每一个事件，映射到这个事件所发生的逻辑时间上：$C: H\longmapsto T​$ ，例如$C(e)​$表示事件$e​$发生的逻辑时间。

下面是评价逻辑时钟系统的两个特性：

  • 一致性
    • 对于两个事件$e_i$和$e_j$，如果$e_i \rightarrow e_j \Rightarrow C(e_i) < C(e_j)$，则这个逻辑时钟系统是一致的。
    • 一致性是逻辑时钟系统必须满足的特性，否则该系统不具有可用性。
  • 强一致性
    • 对于两个事件$e_i$和$e_j$，如果$e_i \rightarrow e_j \Leftrightarrow C(e_i) < C(e_j)$，则这个逻辑时钟系统是强一致的。
    • 强一致性不是逻辑时钟系统必须满足的，但强一致性能让我们根据两个事件发生的逻辑时钟，推断出它们是否依赖。

逻辑时钟系统中，时间分为本地时间和全局时间，这里的全局时间不是真正意义上的全局的时间，而是每一个进程视图下的全局时钟，不意味着所有进程上的全局时钟都完全相同。

时间需要前进，在逻辑时钟系统中，时钟的前进是由事件驱动的：

R1规则：对应本地发生的事件

  • 一个进程发生一个本地事件的时候，进程如何更新自己的本地时间。

R2规则：对应消息传递事件

  • 当进程发送一个消息时，如何将自己视图中的全局时钟附加到消息中，促使目标进程的时钟推进。
  • 当进程接收到一个消息时，如何使用消息中附加的“发送进程视图的全局时钟”推进自己的全局时钟。

时间可以由不同的方式表示，时间表示结构有：

  1. 标量时间
  2. 向量时间
  3. 矩阵时间
  4. …

下面具体介绍标量时间和向量时间。

标量时间

标量时间，顾名思义就是由一个标量表示的时间，通常就是一个整数。我们用$C_i$表示进程$p_i$的逻辑时钟。

使用标量时钟的时候，本地时钟和全局时钟的值是相等的。

对于R1规则：进程$p_i$本地时间的更新：$C_i = C_i + 1$

对于R2规则：

  • 消息发送：当进程$𝑝_𝑖$发送一个消息时，将逻辑时钟$C_𝑖$附加到消息中（算一种本地事件，本地时钟在消息完成发送之前就已经更新）
  • 消息接收：当进程$𝑝𝑖$接收到一个消息，且消息携带的逻辑时钟为$C{𝑚𝑠𝑔}$，更新逻辑时钟$C_𝑖=max⁡(𝐶𝑖, 𝐶{𝑚𝑠𝑔})+1$

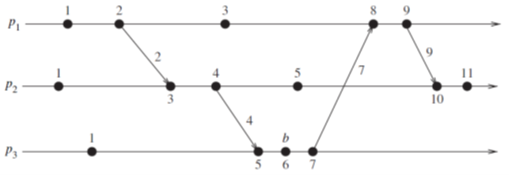
标量时钟更新

标量时间的性质

标量时间是具有一致性的，因为当$e_i \rightarrow e_j$ 成立的时候，有一条从事件$e_i$到事件$e_j$的路径，这个路径中水平的部分(内部事件)，和倾斜的部分(消息传递事件)都会使得逻辑时间增加，就能推出$C(e_i) < C(e_j)$。

但标量时间不具有强一致性，因为标量集合是全序的，而并不是所有事件发生的先后顺序都能够确定，所以很容易就能找出$C(e_i) < C(e_j)$但是$e_i \nrightarrow e_j$。在上图中，$e_1^3 \nrightarrow e_2^4$，但是$C(e_2^4) < C(e_1^3)$。

标量时间可以对数据进行计数，如果事件$e$对应的逻辑时间戳为$h$，则说明到达事件$e$的所有依赖路径中，最长的路径为$h$，$h-1$被称为事件$e$的高度。

向量时间

  1. 每个进程$p_i$维护一个向量$vt_i[1…n]$，$n$为总进程数，$vt_i$是进程$p_i$的全局时间。
  2. $vt_i[x]$是进程$p_i$所掌握的进程$p_x$的本地时间（不一定是最新的），$vt_i[i]$就是进程$p_i$的本地时间。

对于R1规则：$vt_i[i] = vt_i[i] + 1$

对于R2规则：

  • 消息发送：当进程$𝑝_𝑖$发送一个消息时，将全局时钟$vt_i$顺带发送给接收方（发送之前已经使用R1规则）。
  • 消息接收：当进程$𝑝_𝑖$接收到一个消息，且携带的全局时钟是$vt$
    1. 对于$1 \le k \le n : vt_i[k] = max(vt_i[k], vt[k])$, 将全局时钟更新。
    2. 使用R1规则。

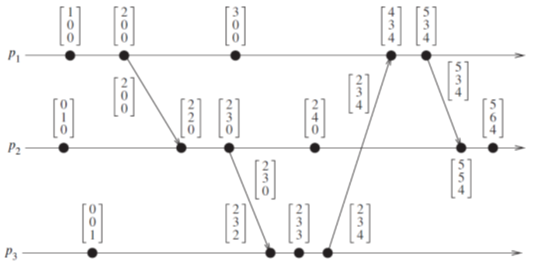
1552581103342

向量时间的比较规则：

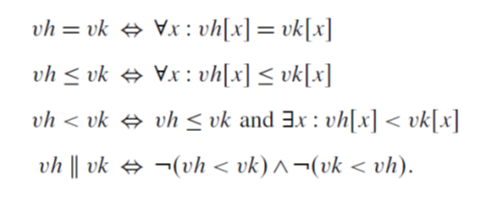
1552581163643

向量时间的性质

向量时间具有一致性，由标量时间的一致性可以很好的得到。

向量时间具有强一致性，如果有 $vh < vk​$,记$vh​$为进程$p_i​$上事件$h​$的时间戳，$vk​$为进程$p_j​$上事件$k​$的时间戳。由定义可得$vh[i] \le vk[i]​$，而$vh[i]​$进程$p_i​$的本地时间，进程$p_j​$全局时间里的值要大于等于$p_i​$的本地时间，根据更新规则，肯定有一条从$h \rightarrow k​$的路径。

事件计数：假定时间e的时间戳为$vt[1…n]$

  • $vt[j]$表示进程$p_j$上因果关系优于e的事件总数。
  • $\sum_{k=1}^n vt[n] - 1$表示在整个计算系统中因果关系先于e的事件总数。

向量时间压缩

当总进程数特别大的话，传递消息附加全局向量时间的成本就会很高（标量时间用4字节的整数来存储的话，1k个进程的全局时间就有4k了）。一个方法是：仅仅发送$vt - vt_{lastsend}$，如果很少改变的话用游长编码就能很好地压缩消息。但是这样需要$O(n^2)$的存储空间。

下面是改进方法：

进程$p_i$维护两个向量：

  • $LastSend_i[1…n]$，其中$LastSend_i[j]$表示进程$p_i$上次给进程$p_j$发送消息时的本地时间。
  • $LastUpdate_i[1…n]$，其中$LastSend_i[k]$表示进程$p_i$上次更新$vt_i[k]$ 时的本地时间。

当$p_i$需要给进程$p_j$发送消息时，以下向量元素需要发送给进程$p_j$

  • 如果$LastSend_i [j]<LastUpdate_i [x]$，则第$x$个向量元素需发送到$p_j$。
  • 这是因为上面条件的成立说明上次给$p_j$发完消息之后，观测到的进程$p_x$的本地时间更新了，要将这个时间发给$p_j$让它更新。

NTP时钟同步

假定两个时钟之间的偏差是$O$，采用如下方法估计$O$。

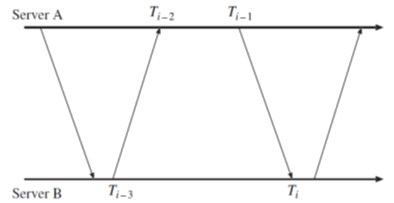
1552616425880

$T_{i-3}$到$T_i-2$之间的传递时间为$t$，$T_{i-1}$到$T_i$之间的传递时间为$t’$，有：

  1. $T_{i-2} = T_{i-3} + t + O$
  2. $T_{i} = T_{i-1} + t’ - O$

由（1） - （2）可得：
$$
O = \frac{T_{i-2} - T_{i-3} + T_{i - 1} - T_i}{2} + \frac{t’ - t}{2}
$$
在很短的时间内，我们可以近似认为$t’ - t$等于0，使用加号左边的式子作为$O$的估计，这时候误差的绝对值$|\frac{t’ -t}{2}| \le |\frac{t’ + t}{2}|$，$t + t’$确定了误差的上界。由(1) + (2)可得：
$$
t + t’ = (T_{i} - T_{i-3}) - (T_{i - 1} - T_2)
$$
NTP同步方法：

发送8次交互信息，以$ (T_{i} - T_{i-3}) - (T_{i - 1} - T_2)$最小的参数为基础，计算$O$的值。

Posted on Edited on

(带补充完整)

设置输出最小宽度

setw(n)对应的只是宽度的最小值，如果要输出的长度本身就超过n则不起作用。当宽度小于最小值的时候，left是添加填充字符到右，right是添加填充字符到左，而internal是添加填充字符到内部选定点。 left 与 right 应用到任何输出，而 internal 应用到整数、浮点和货币输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//来源：https://zh.cppreference.com/w/cpp/io/manip/left
//Left fill:
-1.23*******
0x2a********
USD *1.23***
 
//Internal fill:
-*******1.23
0x********2a
USD ****1.23
 
//Right fill:
*******-1.23
********0x2a
***USD *1.23

设置浮点数精度

setprecision(n)单独使用，精度n指的是整个浮点数的位数，而不是小数的位数，如果浮点数的整数部分位数大于n，那么会采用科学计数法输出，保证n位。

setprecision(n)与fixed(用定点记法生成浮点类型)同时使用，输出浮点数的小数位数就是n了（为什么会这样还不清楚）。定点数的解释

1
2
3
4
5
6
7
8
9
10
11
12
double x = 131235.1415, y = 3.14159;
cout << setprecision(4);
//整个浮点数保留4位
cout << x << endl; //1.312e+005
cout << y << endl; //3.142

cout << fixed;
// 小数部分保留4位
cout << x << endl;//131235.1415
cout << y << endl;//3.1416


Posted on Edited on

原文转自 https://www.cnblogs.com/lvchaoshun/p/7806248.html （修改、增加部分内容）

一 函数指针介绍

函数指针指向某种特定类型，函数的类型由其参数及返回类型共同决定，与函数名无关。举例如下：

1
int add(int nLeft,int nRight);//函数定义

该函数类型为int(int,int),要想声明一个指向该类函数的指针，只需用指针替换函数名即可：

1
int (*pf)(int,int);//未初始化

则pf可指向int(int,int)类型的函数。pf前面有*，说明pf是指针，右侧是形参列表，表示pf指向的是函数，左侧为int，说明pf指向的函数返回值为int。则pf可指向int(int,int)类型的函数。而add类型为int(int,int),则pf可指向add函数。

1
pf = add;//通过赋值使得函数指针指向某具体函数

*注意：pf两端的括号必不可少，否则若为如下定义：**

1
int *pf(int,int);//此时pf是一个返回值为int*的函数，而非函数指针

二 标准C函数指针

1 函数指针的定义

1.1 普通函数指针定义

1
int (*pf)(int,int);

1.2 使用typedef定义函数指针类型

1
2
3
typedef int (*PF)(int,int);
//此时，PF为指向某种类型函数的函数指针类型，而不是具体指针，用它可定义具体指针 
PF pf;

2 函数指针的普通使用

1
2
3
pf = add;  
pf(100,100);//与其指向的函数用法无异  
(*pf)(100,100);//此处*pf两端括号必不可少

注意：add类型必须与pf可指向的函数类型完全匹配

3 函数指针作为形参

1
2
3
4
5
6
//第二个形参为函数类型，会自动转换为指向此类函数的指针  
Void fuc(int nValue,int pf(int,int));  
  
//等价的声明，显示的将形参定义为指向函数的指针  
Void fuc(int nValue,int (*pf)(int,int));  
Void fuc(int nValue,PF);

形参中有函数指针的函数调用，以fuc为例：

1
2
3
pf = add;//pf是函数指针  
fuc(1,add);//add自动转换为函数指针  
fuc(1,pf);

4 返回指向函数的指针

4.1 使用typedef定义的函数指针类型作为返回参数

1
PF fuc2(int);//PF为函数指针类型

4.2 直接定义函数指针作为返回参数

1
int (*fuc2(int))(int,int);//显示定义

说明：按照有内向外的顺序阅读此声明语句。fuc2有形参列表，则fuc2是一个函数，其形参为fuc2(int),fuc2前面有，所以fuc2返回一个指针，指针本身也包含形参列表（int，int），因此指针指向函数，该函数的返回值为int.*

总结：fuc2是一个函数，形参为(int),返回一个指向int(int,int)的函数指针。

三 C++函数指针

1 由于C++完全兼容C，则C中可用的函数指针用法皆可用于C++

2 C++其他函数(指针)定义方式及使用

2.1 typedef与decltype组合定义函数类型

1
typedef decltype(add) add2;

decltype返回函数类型,add2是与add相同类型的函数，不同的是add2是类型，而非具体函数。

1
2
// 使用方法
add2* pf;//pf指向add类型的函数指针，未初始化

2.2 typedef与decltype组合定义函数指针类型

1
2
typedef decltype(add)* PF2;//PF2与1.1PF意义相同  
PF2 pf;// pf指向int(int,int)类型的函数指针，未初始化

2.3 使用推断类型关键字auto定义函数类型和函数指针

1
2
auto pf = add;//pf可认为是add的别名(个人理解)   
auto *pf = add;//pf为指向add的指针

3 函数指针形参

1
2
3
4
typedef decltype(add) add2;  
typedef decltype(add)* PF2;  
void fuc2 (add2 add);//函数类型形参，调用自动转换为函数指针  
void fuc2 (PF2 add);//函数指针类型形参，传入对应函数(指针)即可

说明：不论形参声明的是函数类型：void fuc2 (add2 add);还是函数指针类型void fuc2 (PF2 add);都可作为函数指针形参声明，在参数传入时，若传入函数名，则将其自动转换为函数指针.

4 返回指向函数的指针

4.1 使用auto关键字

1
auto fuc2(int)-> int(*)(int,int) //fuc2返回函数指针为int(*)(int,int)

4.2 使用decltype关键字

1
decltype(add)* fuc2(int)//明确知道返回哪个函数，可用decltype关键字推断其函数类型

5 成员函数指针

5.1普通成员函数指针使用举例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class A//定义类A  
{  
private:  
    int add(int nLeft, int nRight)  
    {  
        return (nLeft + nRight);  
    }  
public:  
    void fuc()  
    {  
        printf("Hello  world\n"); 
    }  
};  
  
typedef void(A::*PF1)();//指针名前需加上类名限定  

PF1 pf1 = &A::fuc; //必须有&  
  
A a;//成员函数地址解引用必须附驻与某个对象地址，所以必须创建一个队形  
  
(a.*pf1)();//使用成员函数指针调用函数

5.2继承中的函数指针使用举例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class A  
{  
public:  
    void fuc()  
    {  
        printf("Hello fuc()\n");  
    }  
    void fuc2()  
    {  
        printf("Hello A::fuc2()\n");  
    }  
};  
  
class B:public A  
{  
public:  
    void fuc2()  
    {  
        printf("Hello B::fuc2()\n");  
    }  
  
};  
typedef void(A::*PF1)();  
typedef void(B::*PF2)();  

PF1 pf1 = &A::fuc;  
  
int main()         
{  
    A a;  
    B b; 
    (a.*pf1)();  //调用A::fuc  
    (b.*pf1)();   //调用A::fuc  

    pf1 = &A::fuc2;  
    (a.*pf1)();  //调用A::fuc2  
    (b.*pf1)();  //调用A::fuc2  

    PF2 pf2 = &A::fuc2;   
    (b.*pf2)(); //调用A::fuc2

    PF2 pf3 = &B::fuc2;
    (b.*pf3)(); // 调用B::fuc2    
}

6 重载函数的指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class A  
{
public:  
    void fuc()  
    {
        printf("Hello fuc()\n");
    }
    void fuc(int a) {
        printf("Hello A::fuc(int)\n");
    }
};  
typedef void(A::*PF1)();   
typedef void(A::*PF2)(int);
PF1 pf1 = &A::fuc; //pf1 指向fuc()
PF2 pf2 = &A::fuc; //pf2 指向fuc(int)
int main()         
{  
    A a;  
    (a.*pf1)(); //Hello fuc()
    (a.*pf2)(0);//Hello A::fuc(int)
    return 0;				
}

Posted on Edited on

类模板

1
2
3
4
5
6
7
8
9
10
11
// 声明
template<typename T>
class A {
public:
	T value;
	...
};

//使用
A<int> object1;
A<double> object2;

在实现方面，编译器通过传进来的参数，生成两份class A的代码。

函数模板

1
2
3
4
5
6
7
8
9
// 声明
template<typename T>
const T& min(T arg) {const T&a, const T& b} {
    return b < a ? b : a;
}

// 使用
cout << min(2, 3);
cout << min(2.4, 3.5);

使用函数模板的时候，不需要先声明传递进去的类型，编译器会进行实参推导。

成员模板

1
2
3
4
5
6
7
8
9
10
11
template <class T1, class T2>
struct some_struct {
		
		T1 a;
		T2 b;
		some_struct(T1 arg1, T2 arg2)
		    :a(arg1), b(arg2) {}
		template <class U1, class U2>
		some_struct(const some_struct<U1, U2>& p)
			: a(p.a), b(p.b) {}
}

模板里面的成员本身又是一个模板，这里成员模板使得子类能够作为参数去构建父类，如：

1
2
3
4
5
6
7
8
9
10
11
12
13
class A {
    ...
}

class B :public A {
    ...
}
B b1;
B b2;
some_struct<B, B> temp1(b1, b2);
some_struct<A, A> temp2(temp1); 
// 此时T1，T2是A;U1，U2是B 
//如果不写成员模板就无法实现这样的操作

模板特化

特化是泛化的反面，是对于模板某些独特的类型做特殊的设计。特化需要整个特化，不能只特化原来模板的一部分。

1
2
3
4
5
6
7
8
9
template <class T>
struct hash {
    ...
}

template<>
struct hash<char> {
    ...
}

模板偏特化

分两种情况，一种是参数个数上的偏特化，指的是模板的参数只特化前面一部分（不能有间隔，只特化第1,3,5参数是错误的）。

例如在标准库中（旧），当vector的第一个模板参数是bool的时候，如果大量的bool值都用原本的一个byte来存储有些不经济，于是对于bool这种情况单独处理。

1
2
3
4
5
6
7
8
9
10
template <typename T, typename Alloc=...>
class vector {
	...
}

template<truename Alloc=...>
class vector<bool, Alloc> {
	...
}

第二种是范围上的偏特化。

1
2
3
4
5
6
7
8
9
10
template <typename T>
class C {
	...
}

// T的范围由原来的任意类型，特化到只能是指针，范围缩小
template <typename T>
class C<T*> {
	...
}

参考

侯捷 c++程序设计

Posted on Edited on

C++ point-like class

point-like class就是行为像指针的类。point-like class的成员中一定有一个真正的指针，class通过重载 *和->等指针的操作来实现pointer-like。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//定义
template<typename T>
class shared_ptr {
public:
	shared_ptr(T* p): ptr(p) {
		...
	}
	T& operator *() {
		return *ptr;
	}
	T* operator ->() {
		return ptr;
	}
private:
	T* ptr;
};
//使用
class object {
public:
	...
	void some_method(){...}
};
object temp;
shared_ptr<object> pointer(&temp);

pointer->some_method(); 
/*
->的重载在C++中比较特殊，pointer-> 在调用了->之后，返回来的ptr仍然会使用->作用到some_method;
(*pointer).some_method();
*/

pointer-like class的例子：STL的迭代器，C++11的智能指针。

function-like class

function-like class 就是类能像函数一样通过括号传入参数执行，重点就在重载括号。也被称为仿函数。

1
2
3
4
5
template <class T>
class Identify {
public:
	const T& operator() (const T& x ){return x;}
};

参考

侯捷 c++程序设计