分布式系统中逻辑时钟与物理时钟的同步
逻辑时钟系统的概念
在分布式系统中,因为网络的延迟,两台计算机无法拥有一致的时钟(每台计算机之间的时钟看上去只有微小的偏差,但在现代计算机CPU以GHZ为单位计算的频率面前,就是无法容忍的误差了),由于无法拥有一致的时钟,人们使用逻辑时钟来表达,记录分布式系统中的时间。
一个逻辑时钟系统由一个时间域$T$和映射关系$C$组成。
- T是一个集合,它包含了所有事件发生的逻辑时间,在分布式系统中并不是所有的事件的发生都确定先后关系,所以集合内的元素一般呈现偏序关系。
- 映射关系$C$将每一个事件,映射到这个事件所发生的逻辑时间上:$C: H\longmapsto T$ ,例如$C(e)$表示事件$e$发生的逻辑时间。
下面是评价逻辑时钟系统的两个特性:
- 一致性
- 对于两个事件$e_i$和$e_j$,如果$e_i \rightarrow e_j \Rightarrow C(e_i) < C(e_j)$,则这个逻辑时钟系统是一致的。
- 一致性是逻辑时钟系统必须满足的特性,否则该系统不具有可用性。
- 强一致性
- 对于两个事件$e_i$和$e_j$,如果$e_i \rightarrow e_j \Leftrightarrow C(e_i) < C(e_j)$,则这个逻辑时钟系统是强一致的。
- 强一致性不是逻辑时钟系统必须满足的,但强一致性能让我们根据两个事件发生的逻辑时钟,推断出它们是否依赖。
逻辑时钟系统中,时间分为本地时间和全局时间,这里的全局时间不是真正意义上的全局的时间,而是每一个进程视图下的全局时钟,不意味着所有进程上的全局时钟都完全相同。
时间需要前进,在逻辑时钟系统中,时钟的前进是由事件驱动的:
R1规则:对应本地发生的事件
- 一个进程发生一个本地事件的时候,进程如何更新自己的本地时间。
R2规则:对应消息传递事件
- 当进程发送一个消息时,如何将自己视图中的全局时钟附加到消息中,促使目标进程的时钟推进。
- 当进程接收到一个消息时,如何使用消息中附加的“发送进程视图的全局时钟”推进自己的全局时钟。
时间可以由不同的方式表示,时间表示结构有:
- 标量时间
- 向量时间
- 矩阵时间
- …
下面具体介绍标量时间和向量时间。
标量时间
标量时间,顾名思义就是由一个标量表示的时间,通常就是一个整数。我们用$C_i$表示进程$p_i$的逻辑时钟。
使用标量时钟的时候,本地时钟和全局时钟的值是相等的。
对于R1规则:进程$p_i$本地时间的更新:$C_i = C_i + 1$
对于R2规则:
- 消息发送:当进程$𝑝_𝑖$发送一个消息时,将逻辑时钟$C_𝑖$附加到消息中(算一种本地事件,本地时钟在消息完成发送之前就已经更新)
- 消息接收:当进程$𝑝𝑖$接收到一个消息,且消息携带的逻辑时钟为$C{𝑚𝑠𝑔}$,更新逻辑时钟$C_𝑖=max(𝐶𝑖, 𝐶{𝑚𝑠𝑔})+1$
标量时间的性质
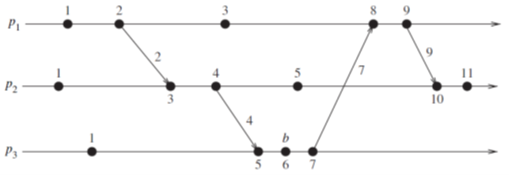
标量时间是具有一致性的,因为当$e_i \rightarrow e_j$ 成立的时候,有一条从事件$e_i$到事件$e_j$的路径,这个路径中水平的部分(内部事件),和倾斜的部分(消息传递事件)都会使得逻辑时间增加,就能推出$C(e_i) < C(e_j)$。
但标量时间不具有强一致性,因为标量集合是全序的,而并不是所有事件发生的先后顺序都能够确定,所以很容易就能找出$C(e_i) < C(e_j)$但是$e_i \nrightarrow e_j$。在上图中,$e_1^3 \nrightarrow e_2^4$,但是$C(e_2^4) < C(e_1^3)$。
标量时间可以对数据进行计数,如果事件$e$对应的逻辑时间戳为$h$,则说明到达事件$e$的所有依赖路径中,最长的路径为$h$,$h-1$被称为事件$e$的高度。
向量时间
- 每个进程$p_i$维护一个向量$vt_i[1…n]$,$n$为总进程数,$vt_i$是进程$p_i$的全局时间。
- $vt_i[x]$是进程$p_i$所掌握的进程$p_x$的本地时间(不一定是最新的),$vt_i[i]$就是进程$p_i$的本地时间。
对于R1规则:$vt_i[i] = vt_i[i] + 1$
对于R2规则:
- 消息发送:当进程$𝑝_𝑖$发送一个消息时,将全局时钟$vt_i$顺带发送给接收方(发送之前已经使用R1规则)。
- 消息接收:当进程$𝑝_𝑖$接收到一个消息,且携带的全局时钟是$vt$
- 对于$1 \le k \le n : vt_i[k] = max(vt_i[k], vt[k])$, 将全局时钟更新。
- 使用R1规则。
向量时间的比较规则:
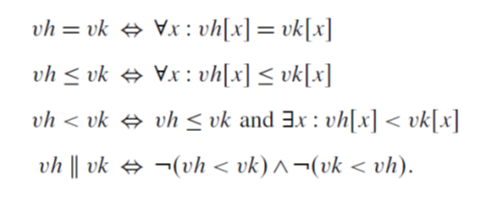
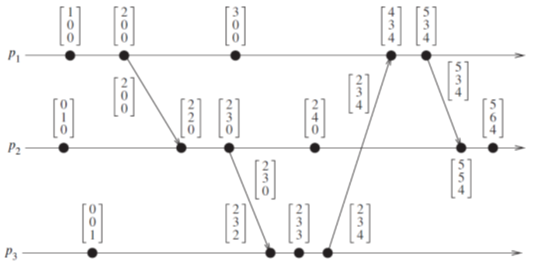
向量时间的性质
向量时间具有一致性,由标量时间的一致性可以很好的得到。
向量时间具有强一致性,如果有 $vh < vk$,记$vh$为进程$p_i$上事件$h$的时间戳,$vk$为进程$p_j$上事件$k$的时间戳。由定义可得$vh[i] \le vk[i]$,而$vh[i]$进程$p_i$的本地时间,进程$p_j$全局时间里的值要大于等于$p_i$的本地时间,根据更新规则,肯定有一条从$h \rightarrow k$的路径。
事件计数:假定时间e的时间戳为$vt[1…n]$
- $vt[j]$表示进程$p_j$上因果关系优于e的事件总数。
- $\sum_{k=1}^n vt[n] - 1$表示在整个计算系统中因果关系先于e的事件总数。
向量时间压缩
当总进程数特别大的话,传递消息附加全局向量时间的成本就会很高(标量时间用4字节的整数来存储的话,1k个进程的全局时间就有4k了)。一个方法是:仅仅发送$vt - vt_{lastsend}$,如果很少改变的话用游长编码就能很好地压缩消息。但是这样需要$O(n^2)$的存储空间。
下面是改进方法:
进程$p_i$维护两个向量:
- $LastSend_i[1…n]$,其中$LastSend_i[j]$表示进程$p_i$上次给进程$p_j$发送消息时的本地时间。
- $LastUpdate_i[1…n]$,其中$LastSend_i[k]$表示进程$p_i$上次更新$vt_i[k]$ 时的本地时间。
当$p_i$需要给进程$p_j$发送消息时,以下向量元素需要发送给进程$p_j$
- 如果$LastSend_i [j]<LastUpdate_i [x]$,则第$x$个向量元素需发送到$p_j$。
- 这是因为上面条件的成立说明上次给$p_j$发完消息之后,观测到的进程$p_x$的本地时间更新了,要将这个时间发给$p_j$让它更新。
NTP时钟同步
假定两个时钟之间的偏差是$O$,采用如下方法估计$O$。
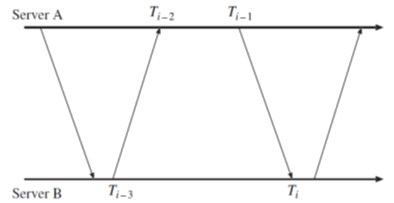
$T_{i-3}$到$T_i-2$之间的传递时间为$t$,$T_{i-1}$到$T_i$之间的传递时间为$t’$,有:
- $T_{i-2} = T_{i-3} + t + O$
- $T_{i} = T_{i-1} + t’ - O$
由(1) - (2)可得:
$$
O = \frac{T_{i-2} - T_{i-3} + T_{i - 1} - T_i}{2} + \frac{t’ - t}{2}
$$
在很短的时间内,我们可以近似认为$t’ - t$等于0,使用加号左边的式子作为$O$的估计,这时候误差的绝对值$|\frac{t’ -t}{2}| \le |\frac{t’ + t}{2}|$,$t + t’$确定了误差的上界。由(1) + (2)可得:
$$
t + t’ = (T_{i} - T_{i-3}) - (T_{i - 1} - T_2)
$$
NTP同步方法:
发送8次交互信息,以$ (T_{i} - T_{i-3}) - (T_{i - 1} - T_2)$最小的参数为基础,计算$O$的值。